规定:update 是树状数组的更新操作,query 是树状数组的查询操作。
P1908 逆序对
题意
给定一段正整数序列,求逆序对的数目。注意序列中可能有重复数字。序列长度 ,序列数字不超过 。
点击查看题解
题解
先离散化,得到各数字的相对大小(求逆序对,与原数字大小没有关系)。
逆序依次对每个数进行 update ,并进行 query。这样,如果一个数对 query 做了贡献,就说明这个数比当前数小,是一对逆序对。
代码
#include<bits/stdc++.h>
using namespace std;
namespace _tree
{
const int N=500000+10;
struct data{int val,pos,rnk;}a[N];
int n,t[N],p=0;
long long ans=0;
int lb(int x){return x&-x;}
int query(int x){int ret=0;while(x>=1)ret+=t[x],x-=lb(x);return ret;}
void update(int x,int y){while(x<=n)t[x]+=y,x+=lb(x);}
void yzmain()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i].val),a[i].pos=i;//Begin of 离散化
sort(a+1,a+1+n,[](data a,data b)->bool{return a.val<b.val;});
for(int i=1;i<=n;i++)
{
if(a[i].val!=a[i-1].val) p++;//保证 val 相同的数,rnk 也相同。
a[i].rnk=p;
}
sort(a+1,a+1+n,[](data a,data b)->bool{return a.pos<b.pos;});//End of 离散化
for(int i=n;i>=1;i--) ans+=query(a[i].rnk-1),update(a[i].rnk,1);
printf("%lld\n",ans);
return;
}
}
int main()
{
_tree::yzmain();
return 0;
}
P1972 [SDOI2009]HH的项链
题意
给定长度为 的序列 , 次询问,每次询问区间 不同的数有多少。,。
点击查看题解
题解
离线 + 树状数组。
将要询问的区间按右端点从小到大排列。如果两个区间右端点相同,则可以把它们放到同一“批次”来讨论。
记录每个数的最后一次出现的位置。随着右端点的向右推移,所记录位置也会改变。如果只有每个数的最后一次出现的位置做 的贡献,就可以方便地得到不同数的个数。可以使用树状数组利用前缀和。
代码
#include<bits/stdc++.h>
using namespace std;
namespace _tree
{
const int N=1000000+10;
struct Q{int l,r,i;}q[N];
int n,m,t[N],a[N],b[N],ans[N];
int lb(int x){return x&-x;}
int query(int x){int ret=0;while(x>=1)ret+=t[x],x-=lb(x);return ret;}
void update(int x,int y){while(x<=n)t[x]+=y,x+=lb(x);}
void yzmain()
{
int l=1,r=1,last=1;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",a+i);
scanf("%d",&m);
for(int i=1;i<=m;i++)
scanf("%d%d",&q[i].l,&q[i].r),
q[i].i=i;
sort(q+1,q+1+m,[](Q a,Q b)->bool{return a.r<b.r;});
while(r<=m)
{
if(q[r].r==q[r+1].r) {r++;continue;}
for(int i=l;i<=r;i++)
{
for(int j=last;j<=q[r].r;j++)
{
if(b[a[j]]) update(b[a[j]],-1);
update(j,1),b[a[j]]=j;
}
ans[q[i].i]=query(q[i].r)-query(q[i].l-1);
}
last=q[r].r;l=r=r+1;
}
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
return;
}
}
int main()
{
_tree::yzmain();
return 0;
}
P1966 [NOIP2013 提高组] 火柴排队
题意
两个盒子分别装有 根火柴,每根火柴都有一个高度(两盒分别为 ,)。 现在将每盒中的火柴各自排成一列。 同一列火柴的高度互不相同。两列火柴之间的距离定义为:。
每列火柴中相邻两根火柴的位置都可以交换,请你通过交换使得两列火柴之间的距离最小。输出这个最小交换次数对 取模的结果。
,。
点击查看题解
题解
证明部分
若规定一根火柴的排名是这根火柴的高度在本列火柴中的第几高,则当对于任何一对火柴,两者排名都相同时, 最小。
显然, 这个式子的值一定不会变化(所有火柴高度的平方和)。所以,当 这个式子取最大值时, 最小。
设 ,,且互不相同,则假设:
得出与题设不同的结论,故假设不成立;又因为四个数互不相同,所以 。
将结论推广。命题得证。
思路部分
首先给初始数据中的火柴按顺序编号。之后给两列火柴按高度排序。排序后,两列火柴之间的距离最小。之后,以任意一列火柴的编号为关键字,给另一列火柴排序,得到另一列火柴的新编号序列。求这个序列的逆序对即可。
理解 1:第一次排序后的局面相当于目标状态,由于由原始状态变为目标状态和由目标状态转为原始状态的步数相同,我们就可以求由目标状态转为原始状态的步数。
“另一列”火柴需要按照新编号顺序排好后,才能达到目标状态。所以求它的逆序对个数,也就是由目标状态转为原始状态(原编号是升序的,所以求逆序对)的步数。
理解 2:只要序列原来对应的火柴排名相同,那么我们排完序(第一次)两数的相对位置不发生改变,因此在第二次排序后另一列火柴的编号序列中不会产生逆序对;一旦对应火柴排名不同,那么这个数是不符合目标状态的,编号序列中对应火柴是逆序的。
代码
#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
const int mod=100000000-3;
struct number{long long value;int num;}ta[5*100000+5],tb[5*100000+5];
struct tree
{
int t[5*100000+5],maxn;
tree(int tmp){memset(t,0,sizeof(t));maxn=tmp;}
int lb(int x){return x&-x;}
void update(int node,int data)
{
for(int i=node;i<=maxn;i+=lb(i))
t[i]+=data;
return;
}
int query(int node)
{
int ans=0;
for(int i=node;i>=1;i-=lb(i))
ans+=t[i];
return ans;
}
};
int n;
long long ans=0,a[5*100000+5];
void yzmain()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&ta[i].value),ta[i].num=i;
for(int i=1;i<=n;i++)
scanf("%lld",&tb[i].value),tb[i].num=i;
sort(ta+1,ta+1+n,[=](number a,number b)->bool{return a.value<=b.value;});
sort(tb+1,tb+1+n,[=](number a,number b)->bool{return a.value<=b.value;});
for(int i=1;i<=n;i++)
a[ta[i].num]=tb[i].num;
tree arr(n);
for(int i=n;i>=1;i--)
{
arr.update(a[i],1);
ans+=arr.query(a[i]-1);
ans%=mod;
}
printf("%lld",ans%mod);
return;
}
}
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
_yz::yzmain();
return 0;
}
P1020 [NOIP1999 普及组] 导弹拦截
题意
给定由 ()个正整数()组成的序列,求其最长不上升子序列和可划分成的子序列(满足序列元素依次不上升)的最少个数。
点击查看题解
题解
另一种方法:link。
求一个序列的最长不上升子序列,相当于将序列反转后,求其最长不下降子序列。
引理:Dilworth 定理,又称狄尔沃斯定理或偏序集分解定理。对于任意有限偏序集,其最大反链中元素的数目必等于最小链划分中链的数目。
此定理的对偶形式亦真。若定义偏序集 ,则链中元素互相可比,反链中元素互不可比。
运用于此题,用的是此定理的对偶形式:最小链划分中链的数目必等于最大反链中元素的数目,即可划分成的不上升子序列的最少个数等于最长上升子序列的长度。
也就是,本题两问转化为,求最长不下降子序列和最长上升子序列的长度。
代码
#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
const int N=100000+10;
int n=1,m=0,a[N],t[N],ans=0;
int lb(int x){return x&-x;}
int query(int x)
{
int ret=0;
while(x>=1)
ret=max(ret,t[x]),x-=lb(x);
return ret;
}
void update(int x,int y)
{
while(x<=m)
t[x]=max(t[x],y),x+=lb(x);
return;
}
void yzmain()
{
while(scanf("%d",a+n)!=EOF)
m=max(m,a[n]),n++;n--;
for(int i=n;i>=1;i--)
{
int now=query(a[i])+1;
ans=max(ans,now);
update(a[i],now);
}
printf("%d\n",ans);ans=0;
memset(t,0,sizeof(t));
for(int i=1;i<=n;i++)
{
int now=query(a[i]-1)+1;//最长上升子序列,不能相等
ans=max(ans,now);
update(a[i],now);
}
printf("%d\n",ans);
return;
}
}
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
_yz::yzmain();
return 0;
}
P3178 [HAOI2015]树上操作
题意
有一棵点数为 的树,以点 为根,且节点有权。然后有 个操作,分为三种:
- 操作 :把某个节点 的点权增加 。
- 操作 :把某个节点 为根的子树中所有点的点权都增加 。
- 操作 :询问某个节点 到根的路径中所有点的点权和。
对于所有数据,,。
点击查看题解
题解
大佬可以使用树链剖分!这里使用 dfs 序和树状数组。
对树进行先序遍历,记录每个点的进栈序和出栈序,根据进出栈序构造树的区间表示,进栈点权为正,出栈点权为负,则点至根的路径点权和转化为前缀和。例子(圆圈中的数字即为点权):
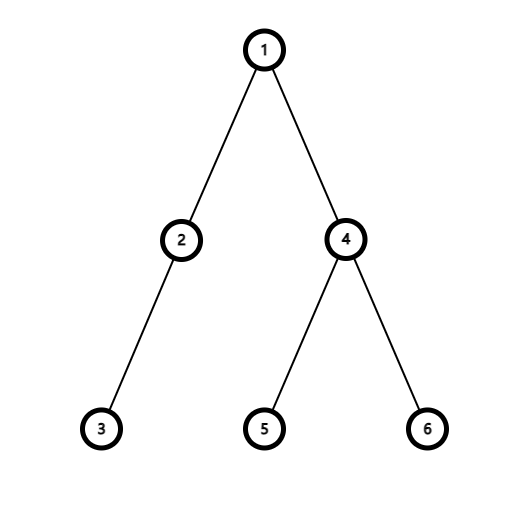
| DFS 序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 对应点权 | 1 | 2 | 3 | -3 | -2 | 4 | 5 | -5 | 6 | -6 | -4 | -1 |
如果我们要求节点 5 到根节点的路径上的点权和,则只需要求到 的前缀和即可。
另外,在 dfs 序中,子孙节点进出栈的位置必定被包含在祖先节点进出栈的位置。比如,节点 5 6 是节点 4 的子孙,则在区间 中包含有 5,-5,6,-6。
所以使用树状数组维护点和区间修改即可。考虑操作对于查询的贡献。
对于操作 1,在原来树上进行单点修改即可。
对于操作 2,若对于以 x 为根的子树修改,节点 y 是节点 x 的后代,那么可以贡献 。
我们可以使用一个树状数组维护单点修改,两个树状数组来维护子树修改(利用差分的思想)。
第一个树状数组维护原点权及单点修改;
第二个树状数组维护 ,第三个树状数组维护 。则利用差分,,再加上第一个树状数组维护的信息,即可求解。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
namespace _yz
{
const int N=1000000+10,Opt_1=0,Opt_2L=1,Opt_2R=2;
struct edge{int nxt,to;}e[N*2];
int n,m,head[N],cnt=0,t[3][N],w[N],in[N],out[N],dfn=0,depth[N];
int lb(int x){return x&-x;}
int query(int x,int type)
{
int ret=0;
for(int i=x;i>=1;i-=lb(i))
ret+=t[type][i];
return ret;
}
void update(int x,int data,int type)
{
for(int i=x;i<=dfn;i+=lb(i))
t[type][i]+=data;
return;
}
void add(int a,int b)
{
e[++cnt]=(edge){head[a],b};
head[a]=cnt;
}
void dfs(int root,int dad)
{
in[root]=++dfn;
for(int i=head[root];i;i=e[i].nxt)
{
int son=e[i].to;
if(son==dad) continue;
depth[son]=depth[root]+1;
dfs(son,root);
}
out[root]=++dfn;
}
void yzmain()
{
int a,b;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
scanf("%lld",w+i);
for(int i=1;i<=n-1;i++)
{
scanf("%lld%lld",&a,&b);
add(a,b),add(b,a);
}
dfs(1,1);
for(int i=1;i<=n;i++)
{
update(in[i],w[i],Opt_1);
update(out[i],-w[i],Opt_1);
}
for(int i=1;i<=m;i++)
{
scanf("%lld",&a);
if(a==1)
{
scanf("%lld%lld",&a,&b);
update(in[a],b,Opt_1);
update(out[a],-b,Opt_1);
}
else if(a==2)
{
scanf("%lld%lld",&a,&b);
update(in[a],b*depth[a],Opt_2L);
update(in[a],b,Opt_2R);
update(out[a],-b*depth[a],Opt_2L);
update(out[a],-b,Opt_2R);
}
else
{
scanf("%lld",&a);
printf("%lld\n",query(in[a],Opt_1) + query(in[a],Opt_2R)*(depth[a]+1)-query(in[a],Opt_2L));
}
}
return;
}
}
#undef int
int main()
{
_yz::yzmain();
return 0;
}
本文作者:Yurchiu
本文链接:https://yz-hs.github.io/13501164c111/
版权声明:本博客中所有原创文章除特别声明外,均允许规范转载,转载请注明出处。所有非原创文章,按照原作者要求转载。

