以下是一些区间 DP 题目，为本蒟蒻在上 luogu 网课时所整理。

P1880 [NOI1995]石子合并

link： P1880 [NOI1995]石子合并。

题面

在一个圆形操场的四周摆放 $N$ 堆石子,现要将石子有次序地合并成一堆。规定每次只能选相邻的 $2$ 堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将 $N$ 堆石子合并成 $1$ 堆的最小得分和最大得分。

$1\leq N\leq100$ ， $0\leq a_i\leq 20$ 。

题解

注意到，合并成的一堆石子一定是一段连续的石子合并而成的。既然是求最值，那么求得的结果满足每一区间都是该区间所能达得到的最值。设 $dp_{i,j}$ 是合并 $[i,j]$ 区间的花费。既然这样，我们就需要将这一圈石子分割为两个子区间。很显然，我们需要枚举一个 $k$ ，来作为这一圈石子的分割线。这样我们就能得到状态转移方程（ $/$ 表示或者）：

dp_{i,j}=\max/\min \{dp_{i,k}+dp_{k+1,j}+\sum_{a=i}^j cost_a \quad |\quad k\in [i,j] \}

因此，要从小长度开始 dp。

由于石子是一圈，可以将输入数列复制为两倍，解决首尾相并问题，这样 ans 是 $\max/\min \{dp_{i,i+n-1} \quad|\quad i\in[1,n]\}$ 。

#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
	const int N=200+5;
	int a[N],n,mn[N][N],mx[N][N],fmn,fmx;
	void yzmain()
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++) scanf("%d",a+i);
		for(int i=1;i<=n;i++) a[i+n]=a[i]; //copy: 1 2 3 1 2 3 解决首尾相并问题
		for(int i=1;i<=n*2;i++) a[i]+=a[i-1];
		
		//dp[i][j]指合并[i,j]的花费
		//dp[i][i]==0
		//dp[i][j]=max{dp[i][k]+dp[k+1][j]+cost(i to j) | k in [i,j]}
		//故需合并小长度
		
		for(int l=2;l<=n;l++) //枚举长度
			for(int i=1,j=l;j<=n*2;i++,j++)
			{
				mn[i][j]=mn[i][i]+mn[i+1][j]+(a[j]-a[i-1]),//其实就是求最值，先存第一个的值，再用以比较。
				mx[i][j]=mx[i][i]+mx[i+1][j]+(a[j]-a[i-1]);
				for(int k=i+1;k<j;k++)
					mn[i][j]=min(mn[i][j],mn[i][k]+mn[k+1][j]+(a[j]-a[i-1])),
					mx[i][j]=max(mx[i][j],mx[i][k]+mx[k+1][j]+(a[j]-a[i-1]));
			}
				
					
		fmn=mn[1][n],fmx=mx[1][n];
		for(int i=2;i<=n;i++)
			fmn=min(fmn,mn[i][i+n-1]),
			fmx=max(fmx,mx[i][i+n-1]);
	
		printf("%d\n%d\n",fmn,fmx);
		return;
	}
}
int main()
{
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	_yz::yzmain();
	return 0;
}

P3146 [USACO16OPEN]248 G

link：P3146 [USACO16OPEN]248 G。

题面

给定一个 $1 \times n $的地图（ $2\leq N\leq 248$ ），在里面玩 2048，每次可以合并相邻两个相等的数（数值范围 $[1,40]$ ），问最大能合出多少。注意合并后的数值并非加倍而是 +1，例如 $2$ 与 $2$ 合并后的数值为 $3$ 。

题解

注意到，合并成的一个数一定是一段连续的数合并而成的。用 $f_{i,j}$ 表示将序列中的第 $i$ 个数合并到第 $j$ 个数全部合并所能得到的最大数值。状态转移方程如下：

f_{i,j}=\max\{f_{i,k}+1\quad|\quad k\in[i,j],f_{i,k}=f_{k+1,j}\not=0\}

只有当左边的部分和右边的部分的数值相同时才能进行转移。

比如说，你有 “7 5 7” 这么一个合并后的东西，显然这两个 “7” 无法合并，但如果你在转移时将 “5” 和 “7” 转移成了 “7” ，你的下一步中两个 “7” 就变的可以合并了，就会出错。

这也就解释了为什么 $f_{1,n}$ 并不一定是最终答案，因为从 $1$ 到 $n$ 并不一定能全部合并，即 $f_{1,n}$ 有可能是 $0$ ，所以在下面的代码中的转移过程中就进行取最终答案的操作。

#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
	int n,a[500],f[500][500],ans=0;
	void yzmain()
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			scanf("%d",a+i),f[i][i]=a[i];
		for(int l=1;l<=n;l++)
			for(int i=1,j=i+l;j<=n;i++,j++)
				for(int k=i;k<=j;k++)
					if(f[i][k]==f[k+1][j]&&f[i][k]&&f[k+1][j])
						f[i][j]=max(f[i][j],f[i][k]+1),
						ans=max(ans,f[i][j]);
		printf("%d\n",ans);
		return;
	}
}
int main()
{
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	_yz::yzmain();
	return 0;
}

P4342 [IOI1998]Polygon

link：P4342 [IOI1998]Polygon。

题面

《Polygon》是一个玩家在一个有 $n$ 个顶点的多边形上的游戏，如图所示，其中 $n=4$ 。每个顶点用整数标记，每个边用符号 $+$ （加）或符号 $*$ （乘积）标记。

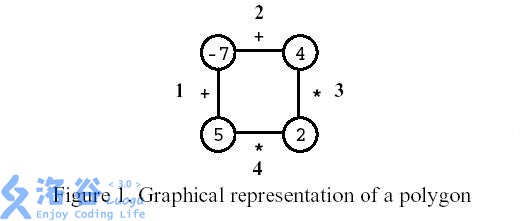
第一步，删除其中一条边。随后每一步：选择一条边连接的两个顶点 $v_i$ 和 $v_j$ ，用边上的运算符计算 $v_i$ 和 $v_j$ 得到的结果来替换这两个顶点。

游戏结束时，只有一个顶点，没有多余的边。如图所示，玩家先移除编号为 $3$ 的边。之后，玩家选择计算编号为 $1$ 的边，然后计算编号为 $4$ 的边，最后，计算编号为 $2$ 的边。结果是 $0$ 。

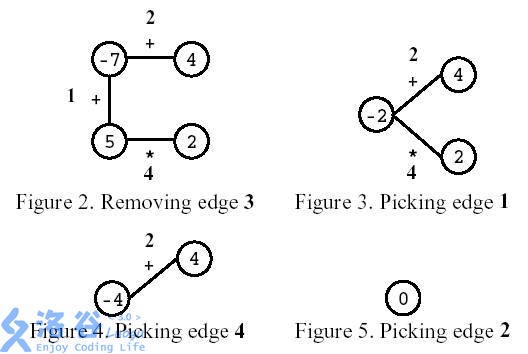
这里每条边的运算符旁边的数字为边的编号，不拿来计算。编写一个程序，给定一个多边形，计算最高可能的分数，及由第一步所删除的一条边开始的方案所得到的此分数（即得到最开始删除的边；可能有多个边满足）。

对于任何一系列的操作，顶点数字都在 $[-32768,32767]$ 的范围内。 $3 \leq n \leq 50$ 。

题解

注意到，合并成的一个数一定是一段连续的数合并而成的。既然第一步要删除其中一条边，那就和石子合并类似，将数列复制为两倍。

设 $f_{i,j}$ 为合并 $[i,j]$ 区间得到的最大数。易得状态转移方程：

f[i][j]=max(f[i][j],f[i][k] opt[k+1] f[k+1][j]);

其中 opt[k+1] 作为运算符。

不过这样是错误的，因为负负也可以得正啊！所以我们还需要维护一个最小值。然后就是分情况讨论的时间：

首先对于加法的情况，因为不存在负负得正一类的情况存在，所以两者的转移方程是基本一样的，大区间的最大值等于合并的两个区间的最大值之和，最小值等于合并的两个区间的最小值之和。

其次对于乘法，这里就很容易有很多遗漏点。请看 code。Yurchiu 已将之排版，利于你理解。

#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
	int n,num[500],mn[500][500]/*最小*/,mx[500][500]/*最大*/,ans;
	char opt[500];
	void yzmain()
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			cin>>opt[i]>>num[i];
		for(int i=1;i<=n*2;i++)
			for(int j=1;j<=n*2;j++)
				mx[i][j]=-114514,mn[i][j]=114514;
		for(int i=1;i<=n;i++)
			mn[i+n][i+n]=mn[i][i]=num[i],
			mx[i+n][i+n]=mx[i][i]=num[i],
			opt[i+n]=opt[i];
		for(int l=2;l<=n;l++)
			for(int i=1,j=l;j<=n*2;i++,j++)
				for(int k=i;k<j;k++)
					if(opt[k+1]=='t')
					{
						mx[i][j]=max(mx[i][j],mx[i][k]+mx[k+1][j]);
						mn[i][j]=min(mn[i][j],mn[i][k]+mn[k+1][j]);
					}
					else
					{
						mx[i][j]=max(mx[i][j],
                                 max(mx[i][k]*mx[k+1][j],
                                     mn[i][k]*mn[k+1][j]
                                 ));
						mn[i][j]=min(mn[i][j],
						         min(mx[i][k]*mx[k+1][j],
								 min(mn[i][k]*mn[k+1][j],
								 min(mx[i][k]*mn[k+1][j],
								     mn[i][k]*mx[k+1][j]
								 ))));
					}
		ans=mx[1][n];
		for(int i=2;i<=n;i++)
			ans=max(ans,mx[i][i+n-1]);
		printf("%d\n",ans);
		for(int i=1;i<=n;i++)
			if(ans==mx[i][i+n-1]) printf("%d ",i);
		return;
	}
}
int main()
{
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	_yz::yzmain();
	return 0;
}

P1043 [NOIP2003 普及组] 数字游戏

题意

在你面前有一圈整数（一共 $n$ 个），你要按顺序将其分为 $m$ 个部分，各部分内的数字相加，相加所得的 $m$ 个结果对 $10$ 取模后再相乘，最终得到一个数 $k$ 。求所得的 $k$ 的最大值及最小值。

点击查看题解

题解

经典区间 DP 题目。易设 $f(i,j,k)$ 表示区间 $[i,j]$ 被分成了 $k$ 段的最大值/最小值。由于数取模后不为负，所以不用考虑负负得正的情况。

然而此题也有一个线性 DP 做法：设 $f(i,j)$ 表示区间 $(i,j]$ 分一段的最大值/最小值。本质上与区间 DP 相同。

代码

区间 DP

#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
	typedef long long ll;
	const ll N=100+10,inf=2147483647;
	ll n,m,c[N],a[N],f[N][N][N],g[N][N][N];
	//f[i][j][k] 表示区间 [i,j] 分了 k 段的最大值
	void dfs(ll l,ll r,ll k)//没加记忆化，因为懒（
	{
		if(r-l+1<=n&&k>m) return;
		if(k==1)
		{
			ll ans=((c[r]-c[l-1])%10+10)%10;
			f[l][r][k]=g[l][r][k]=ans;
			return;
		}
		for(ll mid=l;mid<r;mid++)
		{
			for(ll num=1;num<k;num++)
			{
				if(mid-l+1<num || r-mid<k-num) continue;
				dfs(l,mid,num);dfs(mid+1,r,k-num);
				f[l][r][k]=max(f[l][r][k],
							   f[l][mid][num]*f[mid+1][r][k-num]);
				g[l][r][k]=min(g[l][r][k],
							   g[l][mid][num]*g[mid+1][r][k-num]);
			}
		}
	}
	void solve(ll l,ll r,ll m)
	{
		for(ll k=1;k<=m;k++)
		{
			for(ll i=l;i<=r;i++)
			{
				for(ll j=l;j<=r;j++)
				{
					if(k==1)
					{
						f[i][j][k]=g[i][j][k]=((c[j]-c[i-1])%10+10)%10;
					}
					else
					{
						for(ll mid=i;mid<j;mid++)
						{
							for(ll num=1;num<k;num++)
							{
								if(mid-i+1<num || j-mid<k-num) continue;
								f[i][j][k]=max(f[i][j][k],
											   f[i][mid][num]*f[mid+1][j][k-num]);
								g[i][j][k]=min(g[i][j][k],
											   g[i][mid][num]*g[mid+1][j][k-num]);
							}
						}
					}
				}
			}
		}
	}
	void yzmain()
	{
		ll mn=inf,mx=-inf;
		scanf("%lld%lld",&n,&m);
		for(ll i=1;i<=n;i++)
			scanf("%lld",a+i);
		for(ll i=1;i<=n;i++)
			a[i+n]=a[i];
		for(ll i=1;i<=n+n;i++)
			c[i]=c[i-1]+a[i];
		
		for(ll i=1;i<=n+n;i++)
			for(ll j=1;j<=n+n;j++)
				for(ll k=1;k<=m;k++)
				{
					f[i][j][k]=-inf;
					g[i][j][k]=inf;
				}
		for(ll i=1;i<=n+1;i++)
			solve(i,i+n-1,m);
		for(ll i=1;i<=n+1;i++)
		{
			mn=min(mn,g[i][i+n-1][m]);
			mx=max(mx,f[i][i+n-1][m]);
		}
		printf("%lld\n%lld",mn,mx);
		return;
	}
}
int main()
{
	//freopen("GAME.in","r",stdin);
	//freopen("GAME.out","w",stdout);
	_yz::yzmain();
	return 0;
}
*/

线性 DP

本代码来自 wxf 巨佬，https://www.luogu.com.cn/paste/zgvz75q1。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll; //用long long //yz:不开long long见祖宗
const ll mod=10,inf=5e9;
ll n,m,fmx[505][505],fmn[505][505],num[505],sum[105];
ll maxn=-1e9-5,minn=1e9+5;
int main()
{
	cin>>n>>m;
	for(ll i=1;i<=n;i++)
	{
		cin>>num[i];
		num[i+n]=num[i];
	}
	for(ll i=1;i<=2*n;i++)
	  sum[i]=sum[i-1]+num[i];
	  
	
	for(ll i=0;i<n;i++)
	{
		for(ll ii=0;ii<=m;ii++)
		for(ll j=0;j<=n*2;j++)
		{
			fmx[ii][j]=-inf;
			fmn[ii][j]=inf;
		}
	    for(ll j=1;j<=n;j++)
	    {
		    fmx[1][i+j]=fmn[1][i+j]=(((sum[i+j]-sum[i])%mod)+mod)%mod;
		}
		for(ll j=2;j<=m;j++)
		for(ll k=1;k<n;k++)  //倒数第二段最后一点 
		for(ll p=k+1;p<=n;p++) //最后一段最后一点 //for内变量循环范围一定要符合实际意义 
		{
			
			if(fmx[j][i+p]==-inf) fmx[j][i+p]=fmx[j-1][i+k]*((((sum[i+p]-sum[i+k])%mod)+mod)%mod);
			else fmx[j][i+p]=max(fmx[j][i+p],fmx[j-1][i+k]*((((sum[i+p]-sum[i+k])%mod)+mod)%mod));

			if(fmn[j][i+p]==inf) fmn[j][i+p]=fmn[j-1][i+k]*((((sum[i+p]-sum[i+k])%mod)+mod)%mod);
			else fmn[j][i+p]=min(fmn[j][i+p],fmn[j-1][i+k]*((((sum[i+p]-sum[i+k])%mod)+mod)%mod));
		}
	    maxn=max(fmx[m][n+i],maxn);
	    minn=min(fmn[m][n+i],minn);
	}

	cout<<minn<<endl<<maxn;
	return 0;
}

本文作者：Yurchiu,wxf

本文链接：https://yz-hs.github.io/13809f0fdd1c/

版权声明：本博客中所有原创文章除特别声明外，均允许规范转载，转载请注明出处。所有非原创文章，按照原作者要求转载。

OI 动态规划一些区间 DP

最后更新：2023-08-21, 23:18:21

By Yurchiu.