Yurchiu's Blog
Yurchiu
An AFO whker.
  首页
  归档
158
  标签
81
  分类
24
  说说
  关于
  留言
  链接
  设置

一些关于树的题目

Yurchiu 2021-02-07, 16:31:06 3.1k 隐藏左右两栏 展示左右两栏
首页 / 一些关于树的题目

以下是一些关于树的直径和重心的题目，为本蒟蒻在上网课时所整理。

一些知识

树的直径

定义：树上最长链。

推论，前提是边权非负：

  • 一棵树若存在多条直径，则必然相交于同一点。
  • 任意一点的最远端是树上直径上的一个端点。
  • 若多条直径只有一个公共点，必定互相平均分割。

树的重心

也叫树的质心。

定义：对于一棵树n个节点的无根树，找到一个点，使得把树变成以该点为根的有根树时，最大子树的结点数最小。换句话说，删除这个点后最大连通块（一定是树）的结点数最小。

推论：

  • 树中所有点到某个点的距离和中，到重心的距离和是最小的，如果有两个距离和，他们的距离和一样。
  • 把两棵树通过一条边相连，新的树的重心在原来两棵树重心的连线上。
  • 一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。
  • 一棵树最多有两个重心，且相邻。

VJ 旅游规划(csapc)

题意

给定一棵树，节点数 ≤200000\le 200000，边权均为 11 ，求直径上的点，从小到大输出。

点击查看题解

题解

我们有两种解法。

Solution 1

进行 44 遍搜索（这里用的 44 遍 dfs）。

第一遍：任意选一点（选 00 号点）开始 dfs，求出距离此点最远的点，那样一个直径的端点就被确定了。任意一点的最远端是树上直径上的一个端点。

第二遍：从这个端点 dfs，可求这个直径的另一端点。

第三遍：从任一端点 dfs，设当前 dfs 到的点是 aa，深度是 dad_a ，从 aa 的子树方向的最远点到 aa 的距离是 sas_a，则如果 da+sa=d_a+s_a= 直径，则 aa 就是直径上的点。

第四遍：从另一个端点 dfs，重复以上过程。

为什么要进行第四遍：考虑下面的图。

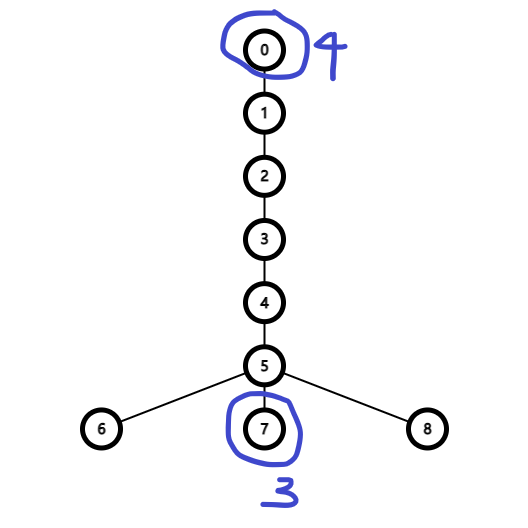
如果我们步骤 33 是从图中蓝色标记 33 的地方开始 dfs，它“两旁”的点就不会计入答案。通过步骤 44，可以计入答案。

如果存在负边权，则此种方法无法得出正确答案。

Solution 2

进行 22 遍 dp。

第一遍：向“下” dp，即 dp 一个点（记为 root）来自其子树方向的最长链和次长链。

第二遍：向“上” dp，即 dp 一个点（记为 son）来自其父亲方向的最长链和次长链。注意不要使得父亲方向的最长链或次长链和来自 son 的子树方向的最长链和次长链重合。

此法任何边权可解。

代码

两个命名空间表示两种做法。

#include<bits/stdc++.h>
using namespace std;
namespace Solution_1
{
    const int N=200000+10;
    struct edge{int nxt,to,len;}e[N*2];
    int n,head[N],cnt=0,jud,one,two,d[N],s[N],len=0,ans[N];
    void add(int x,int y,int len){e[++cnt]=(edge){head[x],y,len};head[x]=cnt;}
    void init()
    {
        memset(d,0,sizeof(d));
        memset(s,0,sizeof(s));
        jud=-1;
    }
    void dfs(int root,int dad,int &var)
    {
        if(jud<d[root]) jud=d[root],var=root;
        for(int i=head[root];i;i=e[i].nxt)
        {
            int son=e[i].to;
            if(son==dad) continue;
            d[son]=d[root]+e[i].len;
            dfs(son,root,var);
            if(len) s[root]=max(s[son]+e[i].len,s[root]);
        }
        if(len) if(s[root]+d[root]==len) ans[root]++;
    }
    void yzmain()
    {
        int t1,t2;
        scanf("%d",&n);
        for(int i=1;i<=n-1;i++)
        {
            scanf("%d%d",&t1,&t2);
            add(t1,t2,1);add(t2,t1,1);
        }
        init();dfs(0,-1,one);
        init();dfs(one,-1,two);
        len=jud;
        init();dfs(one,-1,t1);
        init();dfs(two,-1,t2);
        for(int i=0;i<n;i++) 
            if(ans[i]) printf("%d\n",i);
        return;
    }
}
namespace Solution_2
{
    const int N=200000+10,First=1,Second=2;
    struct edge{int nxt,to,len;}e[N*2];
    int n,head[N],cnt=0,f[N][10],p[N][10],ret[N],dia=0;
    void add(int x,int y,int len){e[++cnt]=(edge){head[x],y,len};head[x]=cnt;}
    void update(int root,int len,int point)
    {
        if(f[root][First]<len)
            f[root][Second]=f[root][First],
            p[root][Second]=p[root][First],
            f[root][First]=len,
            p[root][First]=point;
        else if(f[root][Second]<len)
            f[root][Second]=len,
            p[root][Second]=point;
    }
    int dfsdown(int root,int dad)
    {
        for(int i=head[root];i;i=e[i].nxt)
        {
            int son=e[i].to;
            if(son==dad) continue;
            update(root,dfsdown(son,root)+e[i].len,son);
        }
        return f[root][First];
    }
    void dfsup(int root,int dad,int len)
    {
        update(root,len,dad);
        dia=max(dia,f[root][First]+f[root][Second]);
        for(int i=head[root];i;i=e[i].nxt)
        {
            int son=e[i].to;
            if(son==dad) continue;
            if(son!=p[root][First]) dfsup(son,root,e[i].len+f[root][First]);
            else  dfsup(son,root,e[i].len+f[root][Second]);
        }
    }
    void yzmain()
    {
        int t1,t2;
        scanf("%d",&n);
        for(int i=1;i<=n-1;i++)
        {
            scanf("%d%d",&t1,&t2);
            add(t1,t2,1);add(t2,t1,1);
        }
        dfsdown(0,-1);dfsup(0,-1,-1);
        for(int i=0;i<n;i++) 
            if(f[i][First]+f[i][Second]==dia) printf("%d\n",i);
        return;
    }
}
int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    Solution_CE::yzmain();
    return 0;
}

P4408 [NOI2003] 逃学的小孩

题意

给一棵无根树，选出 AA，BB，CC 三个点使得 AB+BCAB+BC 最大，并保证 BC<ACBC<AC。

点击查看题解

题解

贪心，找直径（设直径端点为 AA，BB），枚举 CC 点，则答案为 max⁡{min⁡{disA,C,disB,C}+disA,B∣C∈V}\max\{\min\{dis_{A,C},dis_{B,C}\}+dis_{A,B} \quad | \quad C \in V\}。这里 VV 是图的点集。

证明请见题解 题解 P4408 【NOI2003 逃学的小孩】。

代码

#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
    const int N=200000+10;
    struct edge{int nxt,to,len;}e[N*2];
    int n,m,head[N],cnt=0,one,two;
    long long jud,d1[N],d2[N],s[N],ans=0,len=0;
    void add(int x,int y,int len){e[++cnt]=(edge){head[x],y,len};head[x]=cnt;}
    void init(long long (&d)[N])
    {
        memset(d,0,sizeof(d));
        memset(s,0,sizeof(s));
        jud=0;
    }
    void dfs(int root,int dad,int &var,long long (&d)[N])
    {
        if(jud<d[root]) jud=d[root],var=root;
        for(int i=head[root];i;i=e[i].nxt)
        {
            int son=e[i].to;
            if(son==dad) continue;
            d[son]=d[root]+e[i].len;
            dfs(son,root,var,d);
            if(len) s[root]=max(s[son]+e[i].len,s[root]);
        }
    }
    void yzmain()
    {
        int t1,t2,t3;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n-1;i++)
        {
            scanf("%d%d%d",&t1,&t2,&t3);
            add(t1,t2,t3);add(t2,t1,t3);
        }
        init(d1);dfs(1,-1,one,d1);
        init(d1);dfs(one,-1,two,d1);
        len=jud;
        init(d1);dfs(one,-1,t1,d1);
        init(d2);dfs(two,-1,t2,d2);
        for(int i=1;i<=n;i++)
        	ans=max(ans,min(d1[i],d2[i])+len);
        printf("%lld\n",ans);
        return;
    }
}
int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    _yz::yzmain();
    return 0;
}

P1395 会议

题意

给出一棵树，节点数 ≤50000\le 50000，求其重心（序号更小的那个）和每个点距离重心的距离和。

点击查看题解

题解

求重心部分：通过重心的定义（删除一个点后最大连通块的结点数最小的点是重心）可以写出以下 dfs 程序。

使用两个数组 st[i] 和 tal[i] 分别表示删除第 ii 号点的最大子树，以第 ii 号点为子树根的大小。

在枚举算符中，st[i] 不会更新到来自 ii 点的父亲方向的子树，所以要用 n−talin-tal_i 即父亲方向的子树大小更新 stist_i。

计算距离部分：设 num[i] 和 d[i] 分别表示以第 ii 号点为子树根的子树节点数，子树所有节点到第 ii 号点的距离和。若一个点为 root，其儿子为 son，则 son 子树所有节点到 root 的距离和 == son 子树所有节点到 son 的距离和 ++ son 子树所有节点数 ×\times root 到 son 的距离。

代码

#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
	const int N=50000+10;
	struct edge{int nxt,to,len;}e[N*2];
	int n,head[N],cnt=0,tal[N],st[N],size,ans,d[N],num[N];
	void add(int x,int y,int len){e[++cnt]=(edge){head[x],y,len};head[x]=cnt;}
	void dfs(int root,int dad)
	{
		for(int i=head[root];i;i=e[i].nxt)
		{
			int son=e[i].to;
			if(son==dad) continue;
			tal[son]=e[i].len;
			dfs(son,root);
			st[root]=max(st[root],tal[son]);
			tal[root]+=tal[son];
		}
		st[root]=max(st[root],n-tal[root]);
	}
	void dis(int root,int dad)
	{
		for(int i=head[root];i;i=e[i].nxt)
		{
			int son=e[i].to;
			if(son==dad) continue;
			num[son]=1;
			dis(son,root);
			d[root]+=d[son]+num[son]*e[i].len;
			num[root]+=num[son];
		}
	}
	void yzmain()
	{
		int t1,t2;
		scanf("%d",&n);
		for(int i=1;i<=n-1;i++)
		{
			scanf("%d%d",&t1,&t2);
			add(t1,t2,1);add(t2,t1,1);
		}
		dfs(1,1);size=st[1];ans=1;
		for(int i=2;i<=n;i++)
		{
			if(size>st[i])
				size=st[i],ans=i;
		}
		dis(ans,ans);
		printf("%d %d",ans,d[ans]);
		return;
	}
}
int main()
{
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	_yz::yzmain();
	return 0;
}

P1364 医院设置

题意

给出一棵二叉树，节点数 ≤100\le 100，点有点权，求其每个点距离重心的距离和。

点击查看题解

代码

这个题当作有点权求重心的模板题吧。无需题解。

#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
	const int N=100+10;
	struct edge{int nxt,to;}e[N*2];
	int n,head[N],cnt=0,tal[N],st[N],d[N],num[N],sum=0;
	void add(int x,int y){e[++cnt]=(edge){head[x],y};head[x]=cnt;}
	void dfs(int root,int dad)
	{
		tal[root]=num[root];
		for(int i=head[root];i;i=e[i].nxt)
		{
			int son=e[i].to;
			if(son==dad) continue;
			dfs(son,root);
			st[root]=max(st[root],tal[son]);
			tal[root]+=tal[son];
		}
		st[root]=max(st[root],sum-tal[root]);
	}
	void dis(int root,int dad)
	{
		for(int i=head[root];i;i=e[i].nxt)
		{
			int son=e[i].to;
			if(son==dad) continue;
			dis(son,root);
			d[root]+=d[son]+num[son];
			num[root]+=num[son];
		}
	}
	void yzmain()
	{
		int t1,t2,t3,size,ans;
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
		{
			scanf("%d%d%d",&t1,&t2,&t3);
			num[i]=t1;sum+=t1;
			if(t2) add(i,t2),add(t2,i);
			if(t3) add(i,t3),add(t3,i);
		}
		dfs(1,1);size=st[1];ans=1;
		for(int i=2;i<=n;i++)
		{
			if(size>st[i])
				size=st[i],ans=i;
		}
		dis(ans,ans);
		printf("%d",d[ans]);
		return;
	}
}
int main()
{
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	_yz::yzmain();
	return 0;
}

X1577 【例 3】数字转换

题意

如果一个数 xx 的约数和 yy （不包括 xx 本身）比 xx 小，那么 xx 和 yy 可以互相转换。例如 44 可以变为 33，11 可以变为 77。给定正整数 nn，限定所有数字转换在不超过 nn 的正整数范围内进行，求不断进行数字转换且不出现重复数字的最多转换步数。1≤n≤500001\le n \le 50000。

点击查看题解

题解

刚看题，感觉这道题和树没有什么关系。不过我们画一下数字转换的路径，这竟然是棵树！

下图为 n=10n=10 时的情况：

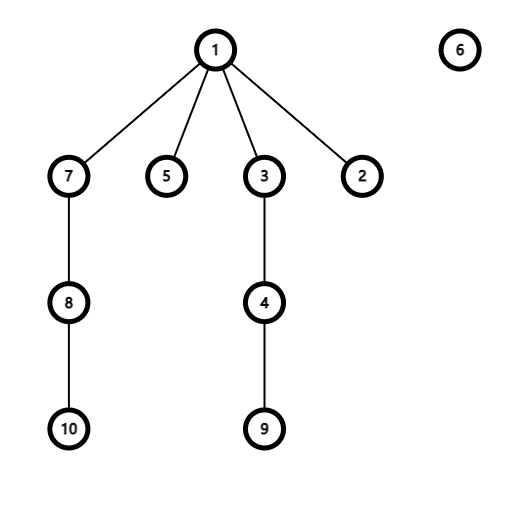
如果设定 yy 是 xx 的前驱，则由于对于每个 xx，它的 yy 值是确定的，这就保证 yy 是 xx 唯一的前驱；且 y<xy<x，这就保证不会出现环。因此数字转换的路径是一棵无根树。

接下来就很显然了：求这棵树的直径大小。

首先预处理出每个 xx 的 yy 值，再连边，即可求直径。

代码

#include<bits/stdc++.h>
using namespace std;
namespace _yz
{
	const int N=50000+10;
	struct edge{int nxt,to;}e[N*2];
	int n,head[N],cnt=0,dis[N],pos,ans;
	queue<int>q;
	void add(int a,int b)
	{
		e[++cnt]=(edge){head[a],b};
		head[a]=cnt;
	}
	void bfs(int st)
	{
		memset(dis,-1,sizeof(dis));
		pos=0,ans=-1;
		q.push(st);dis[st]=0;
		while(!q.empty())
		{
			int now=q.front();q.pop();
			if(dis[now]>ans) ans=dis[now],pos=now;
			for(int i=head[now];i;i=e[i].nxt)
			{
				int to=e[i].to;
				if(dis[to]==-1)
					dis[to]=dis[now]+1,
					q.push(to);
			}
		}
	}
	void yzmain()
	{
		int tmp;
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
		{
			tmp=0;
			for(int j=1;j*j<=i;j++)
			{
				if(i%j) continue;
				tmp+=j;
				if(j!=i/j) tmp+=i/j;
			}
			tmp-=i;
			if(i>tmp&&tmp!=0) add(i,tmp),add(tmp,i),printf("%d: %d\n",i,tmp);
		}
		bfs(1);bfs(pos);//这里使用 bfs 求直径。
		printf("%d\n",ans);
		return;
	}
}
int main()
{
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	_yz::yzmain();
	return 0;
}



本文作者：Yurchiu

本文链接：https://yz-hs.github.io/68f96485e7fc/

版权声明：本博客中所有原创文章除特别声明外，均允许规范转载，转载请注明出处。所有非原创文章，按照原作者要求转载。


OI 树 一些
最后更新：2023-08-21, 23:18:21
By Yurchiu.
最近更新旧文更新
[Works] 自白 终章
《幽默报 10》
AFO 有感
OI 之旅
《幽默报》
[Works] 自白
[Idea] 试卷排序
其他物件杂物收纳
Hitokoto

Yurchiu 说，除了她以外的人都很强！嘤嘤嘤~~
博客信息
文章数目
158
最近更新
08-21
本站字数
350.6k
文章目录

©2019-2023 Yurchiu. All rights reserved.

Theme Cutie, by Yurchiu.