【空间向量】叉积
曾经有人问过我这样一个问题,在求二面角时令两个平面的法向量一个指内一个指外(如下图),就可以保证所求的角是二面角。
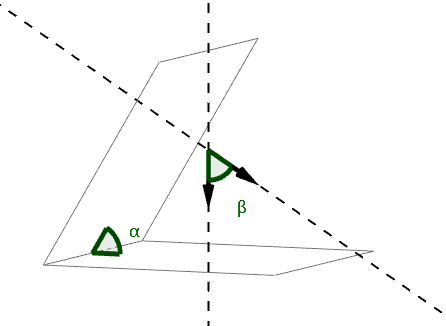
那么如何保证这两个法向量的方向呢?实际上这个问题很简单,观察法就能很好解决。但在这里引出一个概念:叉积(又称叉乘,外积,向量积)。
符号表示:a×b。
二维叉积
叉积的结果是一个向量,并非一个数。
几何意义:二维叉积表示两向量围成的平行四边形的面积(有向面积)。
∣∣∣∣a×b∣∣∣∣=∥∥∥∥a∥∥∥∥b∣∣∣∣sinθ∣∣∣∣
这里 θ 为 a,b的夹角。
计算:点积是数组运算,叉积计算是矩阵运算。所以这里要用到行列式。因为这里只用到二阶和三阶的行列式,因此只简单介绍二阶三阶行列式的运算。
设两不共线向量 i,j 为一组基向量,a=a1i+a2j,b=b1i+b2j。则:
a×b=∣∣∣∣∣a1b1a2b2∣∣∣∣∣=a1b2−a2b1
三维叉积
两个三维向量生成一个新的三维向量。
几何意义,得到的结果是垂直于 a,b所在平面的向量,这个向量的长度是向量 a,b所围成的平行四边形的面积。
方向:根据右手螺旋定则判断方向。
如下图 OA×OB,现将向量移动到同一起点,右手四指从 OA转到 OB,则拇指所指方向,即为结果向量的方向。
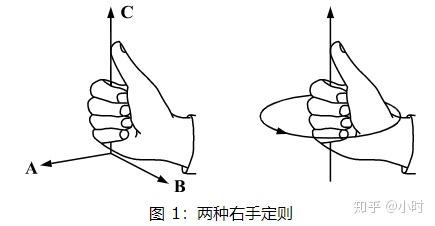
计算
对空间内一组基向量 i,j,k,a=a1i+a2j+a3k,b=b1i+b2j+b3k,
a×b=∣∣∣∣∣∣∣ia1b1ja2b2ka3b3∣∣∣∣∣∣∣=(−1)1+1∣∣∣∣∣a2b2a3b3∣∣∣∣∣⋅i+(−1)1+2∣∣∣∣∣a1b1a3b3∣∣∣∣∣⋅j+(−1)1+3∣∣∣∣∣a1b1a2b2∣∣∣∣∣⋅k=(a2b3−a3b2)i−(a1b3−a3b1)j+(a1b2−a2b1)k
在空间直角坐标系中:a=(a1,a2,a3),b=(b1,b2,b3),a×b=(a2b3−a3b2,−a1b3+a3b1,a1b2−a2b1),有轮换对称的特点。
叉积的运算律
- 反交换律:a×b=−b×a;
- 分配律:a×(b+c)=a×b+a×c;
- 与标量乘法兼容:(λa)×b=a×(λb)=λ(a×b);
- 数乘结合律:(λa)×(μb)=λμ(a×b);
- 向量混合积:(a×b)⋅c=(b×c)⋅a=(c×a)⋅b;
- 两个非零向量平行时,叉积为零向量。
例题
如图,四边形 ABCD 是圆柱底面的内接四边形,AC 是圆柱的底面直径,PC 是圆柱的母线,E 是 AC 与 BD 的交点,AB=AD,∠BAD=60∘。
设点 F 在线段 AP 上,PA=4PF,PC=4CE,求二面角 F−CD−P 的余弦值。
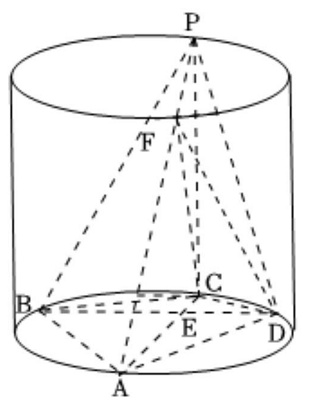
建立如图所示的空间直角坐标系。设 CE=1,则各点坐标为 C(0,0,0),D(1,3,0),P(0,0,4),F(1,0,3)。
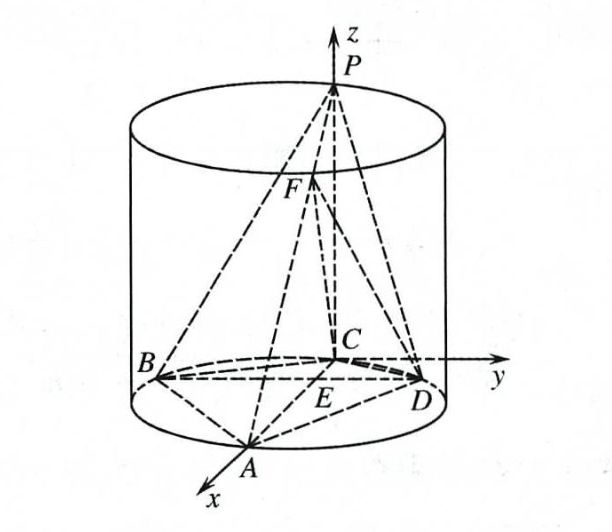
∴CF=(1,0,3),CD=(1,3,0),CP=(0,0,4)
CF×CD=(∣∣∣∣∣0330∣∣∣∣∣,∣∣∣∣∣3011∣∣∣∣∣,∣∣∣∣∣1103∣∣∣∣∣)
∴CF×CD=(−33,3,3),平面 FCD 的法向量可以为 (−3,3,1)。
同理,CP×CD=(−43,4,0),平面 PCD 的法向量可以为 (−3,1,0)。
设二面角 F−CD−P 的平面角为 θ。
cosθ=9+3+1⋅3+143=13239
本文作者:Rhonsua
本文链接:https://yz-hs.github.io/b5c9603ceb3e/
版权声明:本博客中所有原创文章除特别声明外,均允许规范转载,转载请注明出处。所有非原创文章,按照原作者要求转载。
最后更新:2023-08-25, 22:05:41





