题意

link。给定有 $n$ 个正整数的序列，求出一个最优划分（划分出的各个区间称为“段”，第 $i$ 段中数字之和为 $x_i$ ，段数为 $m$ ），满足：

各段连续。
$\forall i \in (1,m]$ ， $x_{i-1}\le x_i$ 。
$\sum\limits_{i=1}^m x_i^2$ 最小。

注意：只有数列给定。~~这么长的原题面就是唬人的~~。

题解

暴搜

枚举划分的段。可得 $24$ 分！

#include<bits/stdc++.h>
using namespace std;
namespace _1 
{
	typedef unsigned long long ull;
	const int N=40000000+10;
	int n,type,pos=0,a[N],b[N];
	ull ANS=4000000000000000000+10;
	void dfs(int step,ull ans,ull pre)
	{
		if(step>=n)
		{
			ANS=min(ANS,ans);
			return;
		}
		if(ans>=ANS) return;
		ull tmp=0,tans=ans;
		for(int i=step+1;i<=n;i++)
		{
			tmp+=a[i];
			if(tmp>=pre) tans+=tmp*tmp,dfs(i,tans,tmp),tans=ans;
		}
	}
	void yzmain()
	{
		scanf("%d%d",&n,&type);
		for(int i=1;i<=n;i++) scanf("%d",a+i);
		a[n+1]=2147483647;dfs(0,0,0);
		printf("%llu\n",ANS);
		return;
	}	
}
int main()
{
	_1::yzmain();
	return 0;
}

动态规划

可以使用 dp 解决部分分。

数轴上的状态设计，好像可以一维dp：设 f[i] 表示以 $i$ 为结尾的最优划分值。不过，它不能保证无后效性。原因：

考虑新加入一个数字，对之前最优划分的影响。发现： $i$ 的加入，不但有可能对 $k-j$ 之间造成影响，也可能会对 $m-j$ 之间产生影响，这就使问题有后效性。

________m________k________j________i

所以，开两维：设 f[i][j] 表示以 $i$ 为结尾的最优划分值，其中最后一段是 $(j,i]$ 。这样就无后效性了。

设 p 是前缀和，则状态转移方程（其中 $i>j>k\ge0$ ， $p(i)-p(j)\ge p(j)-p(k)$ ）：

f(i,j)=min\{f(j,k)\}+[p(i)-p(j)]^2

不加优化，显然 $O(n^3)$ ，可得 $36$ 分。

#include<bits/stdc++.h>
using namespace std;
namespace _2
{
	typedef unsigned long long ull;
	const int N=5000+10;
	const ull OO=4000000000000000000+10;
	ull n,type,pos=0,a[N],p[N],ANS=+OO,f[N][N];
	ull x2(ull x){return x*x;}
	ull min(ull a,ull b){if(a<b) return a;return b;}
	void yzmain()
	{
		ull tmp=0;
		scanf("%llu%llu",&n,&type);
		for(int i=1;i<=n;i++)
			scanf("%llu",a+i),p[i]=p[i-1]+a[i];
		a[n+1]=p[n+1]=+OO;
		for(int i=0;i<=n;i++)
			for(int j=0;j<=n;j++)
				f[i][j]=+OO;
		f[0][0]=0;
		for(int i=0;i<=n;i++)
		{
			for(int j=0;j<i;j++)
			{
				f[i][0]=f[0][0]+x2(p[i]-p[0]);
				for(int k=0;k<j;k++)
				{
					if(p[i]-p[j]>=p[j]-p[k])
						f[i][j]=min(f[i][j],f[j][k]+x2(p[i]-p[j]));
				}
				if(i==n) ANS=min(ANS,f[i][j]);
			}
		}
		printf("%llu\n",ANS);
		return;
	}	
}
int main()
{
	_2::yzmain();
	return 0;
}

贪心

感性的分析：最好的情况是原序列单调递增，划分成 $n$ 段。段越多，结果越好。所以段分得越短越好。

考虑将贪心应用进 DP 的过程中。既然最后一段越短越好，最优解中的最后一段一定是最短的，因此上一段的结尾不再有多种可能性，而是直接选择使最后一段最短的那一个。

f 数组优化一维，时间复杂度优化为 $O(n^2)$ ，可得 $64$ 分。

并没有代码。

单调队列

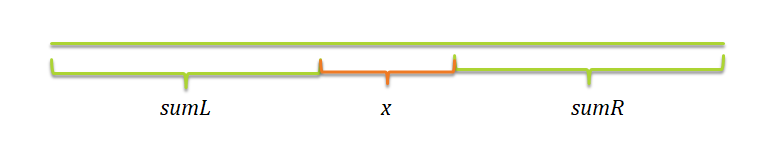
对于图中，分析发现： $x$ 在满足递增的段划分的前提下，越靠前越好。也就是说，最优的情况下与 sumL 合并，使得 sumR 最短。

证明（不完全归纳法）：设 $3$ 段段中数字之和依次分别为 $a$ ， $b$ ， $c$ 。则它们满足： $(a+b)^2+c^2\le a^2+(b+c)^2$ 。

因此，维护一个单调队列。“更优”性已保证单调，因为后加入的一定更优；维护“可行”性的单调性，使之越靠近队尾越不符合前提条件（递增的段划分）。

详情看代码。

时间复杂度优化为 $O(n)$ ，可以获得 $88$ 分。

#include<bits/stdc++.h>
using namespace std;
namespace _3
{
	typedef unsigned long long ull;
	const int N=40000000+10;
	ull n,type,a[N],p[N],f[N],x[N],q[N],head=0,tail=0;
    //a 原数组  p 前缀和  f 以i为结尾的最优划分 x 以i为结尾的最优划分的最后一段划分
    //q 单调队列，元素是数组下标
    //划分段越多越好 -> 段长越短越好 -> 在DP中，最后一段越短越好
	void yzmain()
	{
		scanf("%llu%llu",&n,&type);
		for(int i=1;i<=n;i++)
			scanf("%llu",a+i),p[i]=p[i-1]+a[i];
		for(int i=1;i<=n;i++)
		{
            //在队列中，后边的元素比前面的元素更优，但“更”不满足条件。
            //原因：后面的元素距离 i 更近；在DP中，最后一段越短越好
			while(head+1<=tail && p[i]-p[q[head+1]]>=x[q[head+1]]) head++;
            //如果 head+1 能满足前提条件（划分递增），那 head 就可以弹出了。
            //因为最后一段越短越好。
            //一遍循环后，head 是最优的（后面不满足前提条件）。维护最优时效性。
            x[i]=p[i]-p[q[head]];
            f[i]=f[q[head]]+x[i]*x[i];
            //前提条件：p[i]-p[tail]>=x[tail]
            //移项可得 p[i]>=p[tail]+x[tail]
            //故 p[tail]+x[tail] 是衡量“满足条件”性的标准，越大“越”不满足条件。
            while(head<=tail && p[q[tail]]+x[q[tail]]>=p[i]+x[i]) tail--;
            //维护“满足条件”性的单调性。
            //保证在队列中，后边的元素比前面的元素更优，但“更”不满足条件。
            q[++tail]=i;
		}
		printf("%llu\n",f[n]);
		return;
	}
}
int main()
{
	//freopen("in.txt","r",stdin);
	_3::yzmain();
	return 0;
}

高精度

卡空间！所以我们可以 new 和 delete。
经过分析，发现 f 数组没有必要，因为其他地方用不到 f 数组。因此，我们可以另设数组来存划分的地方，dp 完后再计算答案。
数字太大，使用 __int128（当然比赛不能用，需手写高精度）。

可以获得 $100$ 分。

代码

#include<bits/stdc++.h>
using namespace std;
namespace _4
{
	const int N=40000000+10,M=100000+10;
	__int128 ans=0;
	long long p[N],x[N];
	int f[N],P[M],L[M],R[M],q[N],a,type,n,head=0,tail=0,mod=(1<<30);
	inline long long qread()
	{
		long long s=0,w=1;
  		char ch=getchar();
  		while(ch<'0'||ch>'9')
		{
			if(ch=='-')
				w=-1;
			ch=getchar();
		}
  		while(ch>='0'&&ch<='9')
			s=s*10+ch-'0',ch=getchar();
  		return s*w;
	}
	void yzmain()
	{
		n=qread(),type=qread();
		if(type==1)
        {/*看理解力*/
            int X,Y,Z,m;long long *B=new long long[N];/*C++ 科技*/
            X=qread(),Y=qread(),Z=qread(),B[1]=qread(),B[2]=qread(),m=qread();
            for(int i=1;i<=m;i++)
                P[i]=qread(),L[i]=qread(),R[i]=qread();
            if(n>2) for(int i=3;i<=n;i++) B[i]=(X*B[i-1]+Y*B[i-2]+Z)%mod;
            for(int j=1;j<=m;j++)
                for(int i=P[j-1]+1;i<=P[j];i++)
                    p[i]=B[i]%(R[j]-L[j]+1)+L[j]+p[i-1];
            delete [] B;/*C++ 科技*/
        }
		else for(int i=1;i<=n;i++)
			a=qread(),p[i]=p[i-1]+a;
		for(int i=1;i<=n;i++)
		{
			while(head+1<=tail && p[i]-p[q[head+1]]>=x[q[head+1]]) head++;
            x[i]=p[i]-p[q[head]];
            f[i]=q[head];
            while(head<=tail && p[q[tail]]+x[q[tail]]>=p[i]+x[i]) tail--;
            q[++tail]=i;
		}
		type=n;while(type) ans+=(__int128)/*不加这个东西会导致溢出*/x[type]*x[type],type=f[type];
		int tmp[50];memset(tmp,0,sizeof(tmp));
		while(ans) tmp[++tmp[0]]=ans%10,ans/=10;
		while(tmp[0]) printf("%d",tmp[tmp[0]--]);
		return;
	}
}
int main()
{
	//freopen("in.txt","r",stdin);
	_4::yzmain();
	return 0;
}