线段树，是用来存放给定区间内对应信息的一种数据结构，是一种二叉搜索树。可用来处理数组相应的区间查询和元素更新操作，也可以进行区间最大值，区间最小值或者区间异或值的查询。线段树可以处理很多符合结合律的操作。

线段树是解决区间问题的利器，其核心思想在于分治。

根据维护数值分类：值域线段树、权值线段树。

其他的用法：可持久化线段树、吉如一线段树、李超树、zkm 线段树……

简介

线段树是一种二叉搜索树，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。叶节点数目为 $N$ ，即整个线段区间的长度。子节点不断向自己的父亲节点传递信息，而父节点存储的信息则是他的每一个子节点信息的整合。

线段树的时间复杂度可达 log 级别。而未优化的空间复杂度为 4N 级别，因此有时需要动态开点让空间压缩。

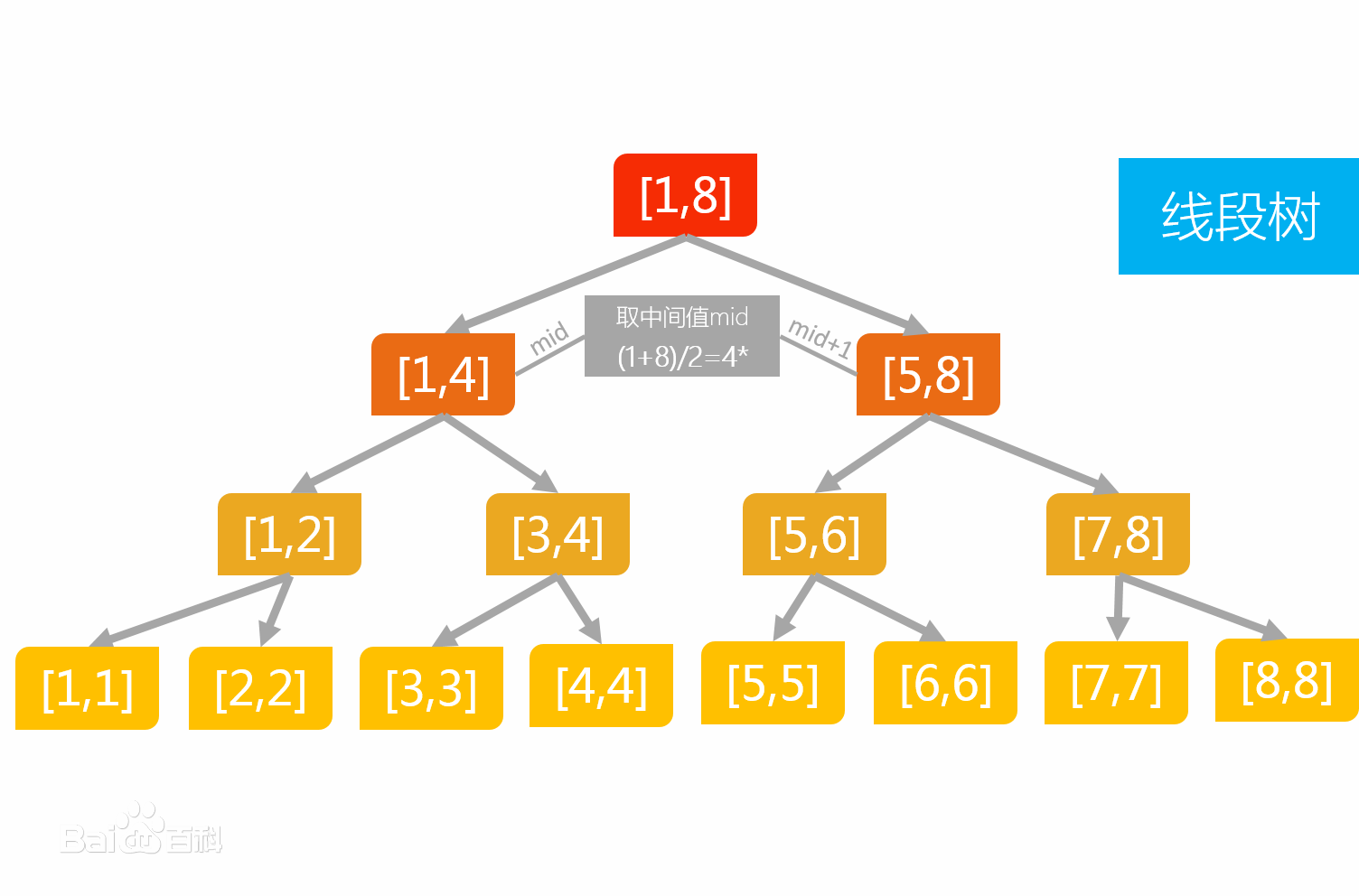
线段树五问

处理较难的线段树问题的常用套路。

维护哪些信息？
维护哪些标记？
如何合并区间信息？
如何快速修改区间信息？
如何合并标记？

以区间加、区间查询为例：

维护哪些信息？区间和。
维护哪些标记？区间加标记。
如何合并区间信息？直接相加。
如何快速修改区间信息？加上增量乘区间长度。
如何合并标记？直接相加。

模板

#1 单点修改、区间查询和

点击查看代码

struct SGT
{
	#define ll long long
	#define lson (root*2)
	#define rson ((root*2)+1)
	#define mid ((l+r)/2)
	ll t[N*4];
	void update(ll root,ll l,ll r,ll pos,ll data)
	{
		if(l==r) {t[root]+=data;return;}
		if(pos<=mid) update(lson,l,mid,pos,data);
		if(pos>mid) update(rson,mid+1,r,pos,data);
		t[root]=t[lson]+t[rson];
	}
	ll query(ll root,ll l,ll r,ll x,ll y)
	{
		if(x<=l&&y>=r) return t[root];
		ll ansl=0,ansr=0;
		if(x<=mid) ansl=query(lson,l,mid,x,y);
		if(y>mid) ansr=query(rson,mid+1,r,x,y);
		return ansl+ansr;
	}
	void build(ll root,ll l,ll r,ll d[])
	{
		if(l==r){t[root]=d[l];return;}
		build(lson,l,mid,d);
		build(rson,mid+1,r,d);
		t[root]=t[lson]+t[rson];
		return;
	}
}Tree;

#2 区间加，区间查询和

线段树要修改很多次，但是很多次修改的值并没有被用到，这几次修改就是无用的，那么我们通过加一个 lazytag 变量（精华，难点），记录当前需要往下传递的数值，待有用时再继续往下传递，这就是 lazytag 思想。

点击查看代码

struct SGT
{
	#define ll long long
	#define lson (root*2)
	#define rson ((root*2)+1)
	#define mid ((l+r)/2)
	struct Node{ll data,tag;}t[N*4];
	void pushdown(ll root,ll l,ll r)
	{
		ll tag=t[root].tag;
		if(t[root].tag==0) return;
		t[lson].data+=tag*(mid-l+1);
		t[rson].data+=tag*(r-mid);
		t[lson].tag+=tag;t[rson].tag+=tag;
		t[root].tag=0;
		return;
	}
	void update(ll root,ll l,ll r,ll x,ll y,ll data)
	{
		if(x<=l&&y>=r)
		{
			t[root].data+=data*(r-l+1);
			t[root].tag+=data;
			return;
		}
		pushdown(root,l,r);
		if(x<=mid) update(lson,l,mid,x,y,data);
		if(y>mid) update(rson,mid+1,r,x,y,data);
		t[root].data=t[lson].data+t[rson].data;
	}
	ll query(ll root,ll l,ll r,ll x,ll y)
	{
		if(x<=l&&y>=r) return t[root].data;
		pushdown(root,l,r);
		ll ansl=0,ansr=0;
		if(x<=mid) ansl=query(lson,l,mid,x,y);
		if(y>mid) ansr=query(rson,mid+1,r,x,y);
		return ansl+ansr;
	}
	void build(ll root,ll l,ll r,ll d[])
	{
		if(l==r){t[root].data=d[l];return;}
		build(lson,l,mid,d);
		build(rson,mid+1,r,d);
		t[root].data=t[lson].data+t[rson].data;
		return;
	}
}Tree;

简单应用

P3372 【模板】线段树 1

link。模板题，就不用说了吧。

P3373 【模板】线段树 2

link。

我们发现一个 lazytag 是不能够解决问题的，那就上两个，分别表示乘法意义上的 lazytag 和加法意义上的 lazytag。紧接着想到 pushdown 操作之后我们又发现必须在向下传递 lazytag 的时候人为地为这两个 lazytag 规定一个先后顺序。可以规定乘法优先。

规定好 tree[son].data=tree[son].data*tree[root].mtag+tree[root].atag*(r-l+1)，这样的话假如改变 atag 的数值就只改变 atag，改变 mtag 的时候把 atag 也对应的乘一下就可以了，没有精度损失，看起来很不错。

P1198 [JSOI2008]最大数

link。

题面

现在请求你维护一个数列，要求提供以下两种操作，共 $M$ 个操作：

查询操作。
- 功能：查询当前数列中末尾 $L$ 个数中的最大的数，并输出这个数的值。
- 限制： $L$ 不超过当前数列的长度。 $(L > 0)$ 。
插入操作。
- 功能：将 $n$ 加上 $t$ ，其中 $t$ 是最近一次查询操作的答案（如果还未执行过查询操作，则 $t=0$ )，并将所得结果对一个固定的常数 $D$ 取模，将所得答案插入到数列的末尾。
- 限制： $n$ 是整数（可能为负数）并且在长整范围内。

注意：初始时数列是空的，没有一个数。

对于全部的测试点，保证 $1 \leq M \leq 2 \times 10^5$ ， $1 \leq D \leq 2 \times 10^9$ 。

题解

这很明显，是单点修改、区间查询最大值，可用线段树解决。

先建立一个叶子节点数为 $M$ 的线段树，叶子节点赋值为极小值。并定义 $len$ 表示数列长度。

插入操作即为修改第 $len+1$ 节点的值，并 $len \gets len+1$ ，单点修改。

查询操作即为查询区间 $[len-L+1,len]$ 的最大值，区间查询。

P1438 无聊的数列

link。

题面

维护一个数列，支持两种操作：

给出一个长度等于 $r-l+1$ 的等差数列，首项为 $K$ ，公差为 $D$ ，并将它对应加到 $[l,r]$ 范围中的每一个数上。即：令 $a_l=a_l+K,a_{l+1}=a_{l+1}+K+D,\ldots ,a_r=a_r+K+(r-l) \times D$ 。
询问序列的第 $p$ 个数的值 $a_p$ 。